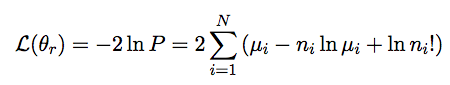
Log likelihood of physics parameters theta_r for a distribution of N bins, n_i observed on mu_i expected.
John Kelley, UW-Madison, May 2008
Our observable in both the new physics and conventional hypotheses is the zenith-angle / energy spectrum of atmospheric muon neutrinos. As an energy proxy, we use the common energy-correlated observable Nch, or number of channels / OMs hit during an event. To quantify agreement / disagreement with a given hypothesis, we use a binned likelihood analysis comparing the cosine of the Pandel-reconstructed zenith angle and the Nch distribution with that predicted by a set of new physics or conventional parameters that we wish to test.
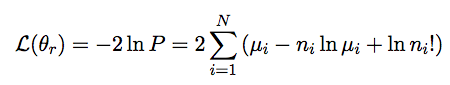
Log likelihood of physics parameters theta_r for a distribution of N bins, n_i observed on mu_i expected.
Feldman and Cousins' paper (physics/9711021) describes how to build central confidence intervals using a likelihood ratio as a test statistic, and gives a relevant example involving conventional neutrino oscillations. The downside is that they do not discuss the problem of how to incorporate systematic errors. We address this by using an extension recommended by Feldman in a Fermilab colloquium called the profile construction method.
The profile likelihood incorporates systematic errors / nuisance parameters by choosing the "worst-case" set of nuisance parameters for a given hypothesis. It is already used in the 'MINOS' error methods of MINUIT; Feldman's method simply applies it to the frequentist construction.
We refer the interested reader to our writeup of this procedure here (PDF).
A note on binning: in general, finer binning is better for a likelihood analysis, to the limit of an unbinned analysis using a continuous PDF; this increase in sensitivity is shown in the following figure.

Figure 3.1: VLI sensitivity (chi2 approximation) versus number of bins in Nch and cos(Zenith)
In practice, though, binning more finely than makes sense for the detector (for example, exceeding the angular resolution) could potentially introduce artifacts from data/MC disagreement. Since the increase in sensitivity is not dramatic after 10x10, we choose the following for the range and binning for our observables:
Parameter |
Low |
High |
# of bins |
cos(Zenith) |
-1.0 |
0.0 |
10 |
Nch |
20 |
120 |
10 |
With regards to the range of the observables chosen: cos(Zenith) is chosen to use only the events below the horizon. The lower end of Nch is set by the multiplicity trigger. We cut off the upper end of the Nch distribution after we drop to the level of a few events at the final cut level -- beyond this, any small high-multiplicity background contribution could significantly distort the likelihood. Expected distributions are shown in the simulation section.