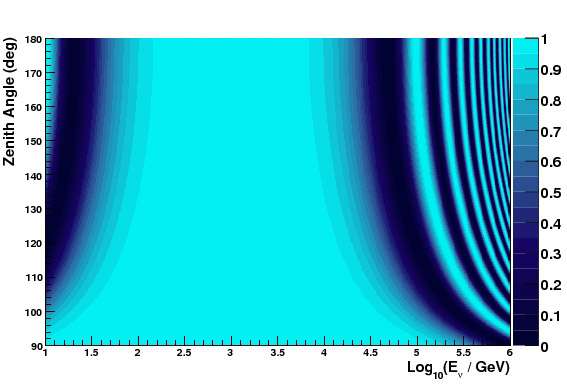
Figure 2.1: Muon neutrino survival probability as a function of energy and zenith angle (conventional + VLI oscillations, delta_c/c = 1e-27)
John Kelley, UW-Madison, May 2008
Neutrino oscillations provide a quantum interferometer sensitive to very small shifts in energy, and can thus act as a sensitive probe of deviations from the Standard Model. These effects are detectable by the same method as standard neutrino oscillations — muon neutrinos generated in the atmosphere change flavor as they propagate to the detector. Because of the different path lengths at different zenith angles, this results in a measurable distortion from the expected zenith angle / energy spectrum. Unlike standard atmospheric oscillations, which decrease with energy and are essentially negligible above 100 GeV, these effects often increase with energy.
Specific models that can be tested with this technique include:
From a practical perspective, we can simulate the new physics (NP) effects simply by weighting atmospheric neutrino events with a muon neutrino survival probability, calculated for the NP model and parameters that we are interested in. For VLI, the observable parameters are:
Parameter |
Range |
Description |
log10(delta_c/c) |
-28 to -24 |
Splitting of VLI eigenstates. Controls what
energy new oscillations turn on. |
sin(2 xi) |
-1 to 1 |
Mixing angle. Controls depth of oscillation minima. |
cos(eta) |
0 or 1 |
Phase between conventional and VLI oscillations
(see below). |
The phase eta is only important when delta_c/c is so large that the VLI and conventional oscillations overlap; however, since AMANDA-II is not sensitive to conventional oscillations, we can safely neglect this parameter and set cos(eta) to zero. This also has the nice side effect that we only have to vary the mixing angle from 0 to pi/4.

Figure 2.1: Muon neutrino survival probability as a function of energy and zenith angle (conventional + VLI oscillations, delta_c/c = 1e-27)
For quantum decoherence, the observable parameters are:
Parameter |
Range |
Description |
log10(gamma_3*), log10(gamma_8*) |
-34 to -27 |
Decoherence threshold 1; lose 1/6 of nu_mu |
log10(gamma_6*), log10(gamma_7*) |
-34 to -27 |
Decoherence threshold 2; lose 1/2 of nu_mu |
Setting all the gamma* parameters to the same value means there is just one threshold at which 1:1:1 decoherence turns on (lose 2/3 of nu_mu). Also, in the survival probability, the gamma* are multiplied by an energy factor which depends on the phenomenology; here we choose an E^2 model.

Figure 2.2: Muon neutrino survival probability as a function of energy and zenith angle (conv. osc. + QD, gamma_i* = 1e-31, E^2 model)
Additional background and theoretical motivation of Lorentz violations is presented in Coleman and Glashow (PRD 59 (1999) 116008) as well as Glashow (hep-ph/0407087). Additional background on quantum decoherence is available in Ellis et al. (Nucl. Phys. B241 (1984) 381-405) and Anchordoqui et al. (hep-ph/0506168).
In the absence of new physics, we can test how well the atmospheric neutrino spectrum agrees with current models, such as Barr et al. ("Bartol", astro-ph/0403630) or Honda et al. ("Honda 2006", astro-ph/0611418). These models have been extrapolated to high energies (above 700 GeV) by T. Montaruli, C. Lewis, and JK in the NeutrinoFlux class. By comparing the predicted zenith angle / energy spectra for these models with data, we can constrain the various models in the AMANDA-II energy region.